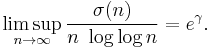5040 (number)

5040 is a factorial (7!), a highly composite number, a superior highly composite number, a colossally abundant number, and the number of permutations of 4 items out of 10 choices (10 × 9 × 8 × 7 = 5040).

5040
List of numbers — Integers ← 1k 2k 3k 4k 5k 6k 7k 8k 9k →
Cardinal	5040 Five thousand [and] forty
Ordinal	5040th Five thousand [and] fortieth
Roman numeral	VXL
Factorization	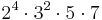$2^4 \cdot 3^2 \cdot 5 \cdot 7$
Divisors	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 24, 28, 30, 35, 36, 40, 42, 45, 48, 56, 60, 63, 70, 72, 80, 84, 90, 105, 112, 120, 126, 140, 144, 168, 180, 210, 240, 252, 280, 315, 336, 360, 420, 504, 560, 630, 720, 840, 1008, 1260, 1680, 2520, 5040
Binary	1001110110000
Duodecimal	2B00
Hexadecimal	13B0

1 Philosophy
2 Number Theory
3 Other
4 5040 and 7920
5 Notes
6 External links

Philosophy

Plato mentions in his Laws that 5040 is a convenient number to use for dividing many things (including both the citizens and the land of a state) into lesser parts. He remarks that this number can be divided by all the (natural) numbers from 1 to 12 with the single exception of 11. He rectifies this "defect" by suggesting that two families could be subtracted from the citizen body to produce the number 5038, which is divisible by 11. Plato also took notice of the fact that 5040 can be divided by 12 twice over. Indeed, Plato's repeated insistence on the use of 5040 for various state purposes is so evident that it is written, "Plato, writing under Pythagorean influences, seems really to have supposed that the well-being of the city depended almost as much on the number 5040 as on justice and moderation."^[1]

Number Theory

If 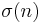$\sigma(n)$ is the divisor function and $\gamma$ is the Euler-Mascheroni constant, then 5040 is the largest known number for which this inequality holds:

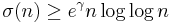$\sigma(n) \geq e^\gamma n\log \log n$ .

This is somewhat unusual, since in the limit we have:

$\limsup_{n\rightarrow\infty}\frac{\sigma(n)}{n\ \log \log n}=e^\gamma.$

Guy Robin showed in 1984 that the inequality fails for all larger numbers if and only if the Riemann hypothesis is true.

Other

▪ 5040 is considered an important number in some systems of numerology, not only because of the Plato connection, but because using round figures, the sum of the radii of both the Earth and Moon (in miles) is 3960 + 1080 = 5040.^[2] Incidentally, the sum of their diameters is also the number of minutes in a week (7 days × 24 hours × 60 minutes = 10,080).

▪ The ratio of the radius of the moon and the radius of the earth is 1080/3960, which simplifies to 3/11. This ratio can also be expressed as (4 - π)/π, when using 22/7 as the value of π. This means that the sizes of the earth and the moon are related by a simple function of π.

▪ Given that the radius of the moon is 3/11 that of the earth, the sum of their radii can be broken into 3/14 (for the radius of the moon) and 11/14 (for the radius of the earth). Further, the sum of their radii in miles is 5040, which when divided by 14 is 360 (the number of degrees in a circle). This would not happen for another pair of objects with radii in the same ratio - it only happens when the sum of their radii is 5040.

▪ 5040 has exactly 60 divisors, counting itself and 1.

▪ In a vigesimal system, 5040 is represented as 12 groups of 20's and 12 groups of 20-squared's (12 • 20 = 240, 12 • 20² = 4800, and 240 + 4800 = 5040).

▪ 5040 is the sum of 42 consecutive primes (23 + 29 + 31 + 37 + 41 + 43 + 47 + 53 + 59 + 61 + 67 + 71 + 73 + 79 + 83 + 89 + 97 + 101 + 103 + 107 + 109 + 113 + 127 + 131 + 137 + 139 + 149 + 151 + 157 +163 + 167 + 173 + 179 + 181 + 191 + 193 + 197 + 199 + 211 + 223 + 227 + 229).

5040 and 7920

▪ As previously stated, 5040 is the product of both 1 × 2 × 3 × 4 × 5 × 6 × 7 and 7 × 8 × 9 × 10. Additionally, 7920 is the product of 8 × 9 × 10 × 11.

▪ The ratio 7920/5040, which is (11!/7!)/7!, or equivalently 11!/(7!)², also equals 11/7. The numbers 11 and 7 are the only pair of natural numbers (along with 3 and 2) for which this occurs: (n!/m!)/m! = n/m; or equivalently: n!/(m!)² = n/m.

▪ The ratio 7920/5040 simplifies to 11/7, which is π/2 (when using 22/7 for π). Similarly, 5040/7920 is 7/11, which is 2/π (when using 22/7 for π).

▪ Given a circle with radius 5040 units, a quarter of that circle's circumference is 7920 units (when using 22/7 for π).

▪ On the 27th of August, 2002, a crop formation was discovered at Crooked Soley in Wiltshire, England that had an outer ring split into 1,296 curved, diamond-like sections. The crops in 504 of those sections were still standing while the crops in the other 792 were leaning virtually horizontally.

Notes

^ Laws, by Plato at Project Gutenberg; retrieved 7 July 2009
^ City of Revelation: On the Proportions and Symbolic Numbers of the Cosmic Temple, by John Michell (ISBN 0-345-23607-6), p. 61.

External links

Mathworld article on Plato's numbers